We are a theoretical biophysics group, interested in a variety of biophysical questions, some more theoretical and others linked to concrete biological problems. We are in particular fascinated by emergent properties at different scales in biological systems, for instance:
1/ How do cytoskeletal elements, which generate forces within cells, self-organise to produce complex spatio-temporal patterns?
2/ how do cells concomitantly acquire identities and shape a tissue during development?
3/ how does complex tissue architecture, such as branched organs, derive from simple local and global rules?
Here are a few examples of concrete problems we have looked or are looking at, often in collaboration with experimental biologists:
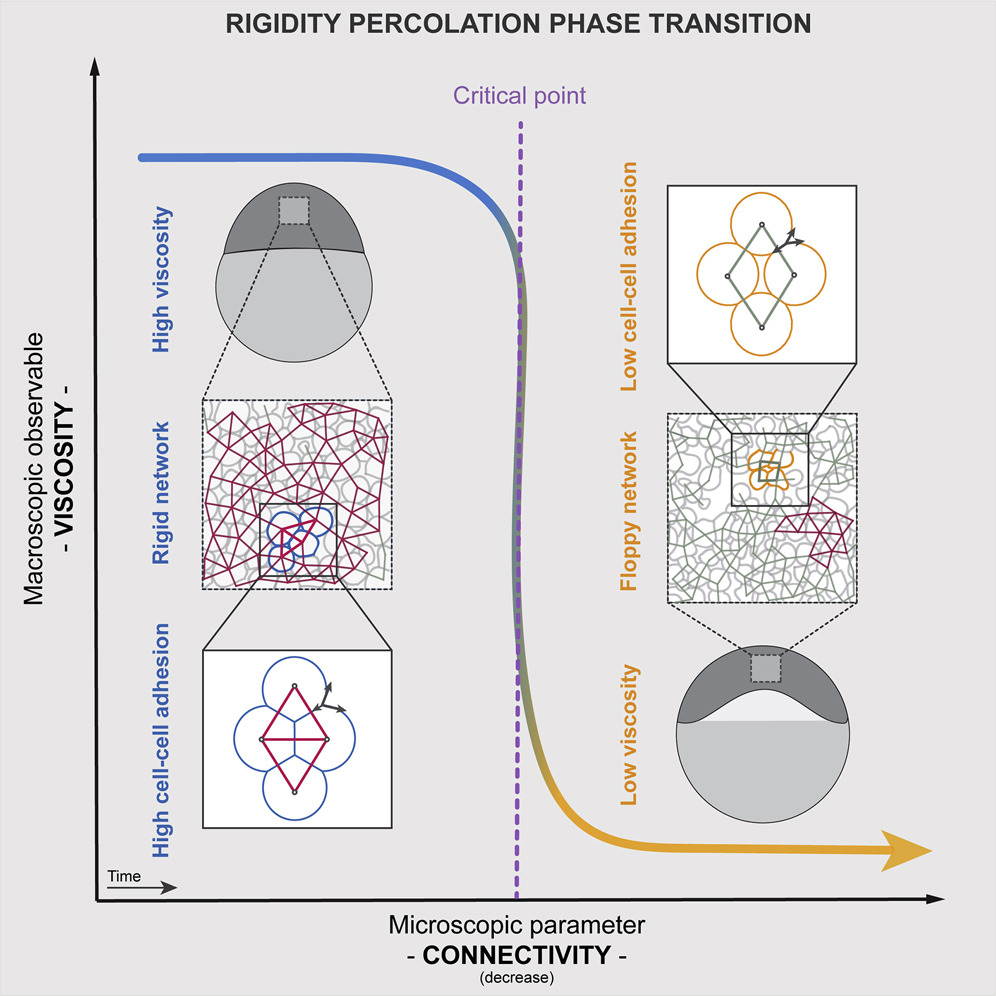
Although rigidity and jamming transitions have been widely studied in physics and material science, their importance in a number of biological processes, including embryo development, tissue homeostasis, wound healing, and disease progression, has only begun to be recognized in the past few years . We have shown that rigidity percolation provides a simple criterion to udnerstand the rheology of non-confluent 3D tissues such as the early zebrafish embryo (Petridou et al, Cell, 2021, Hannezo & Heisenberg, Trends Cell Biol, 2022).
While directional migration often relies on a chemokine gradient generated from a localized source, alternative mechanisms have emerged in the past few years. In particular, self-generated gradients both shaped and sensed by cells themselves are an elegant solution for efficient guidance. We work on understanding how this principle can be coupled to cellular fate during gastrulation (Stock et al, Sci Adv, 2022 or between different immune cell types (Ucar et al, PNAS, 2025).
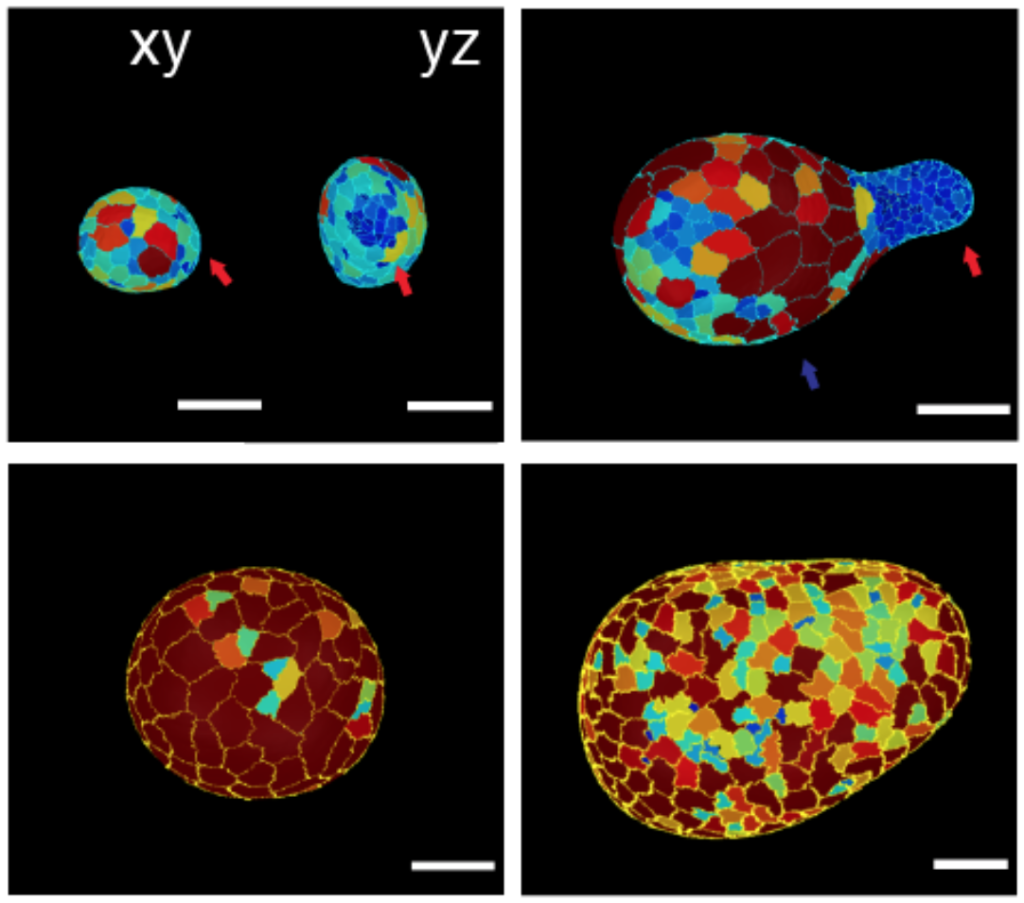
During development, patterns of cellular fate are often set concomitantly to shape and mechanical patterns, begging the question of the respective role of ‘mechanics’ vs ‘chemistry’ as a basis for morphogenesis. We develop models to understand this interplay, both at the continuum level (Recho et al, PNAS, 2019) and using 3D vertex models (Hannezo et al, PNAS, 2015). We apply these theories to embryo and organoid morphogenesis (Yang*, Xue* et al, NCB, 2021, Luciano*, Xue, Nat Phys, 2021, Pinheiro et al, Nat Phys, 2022).
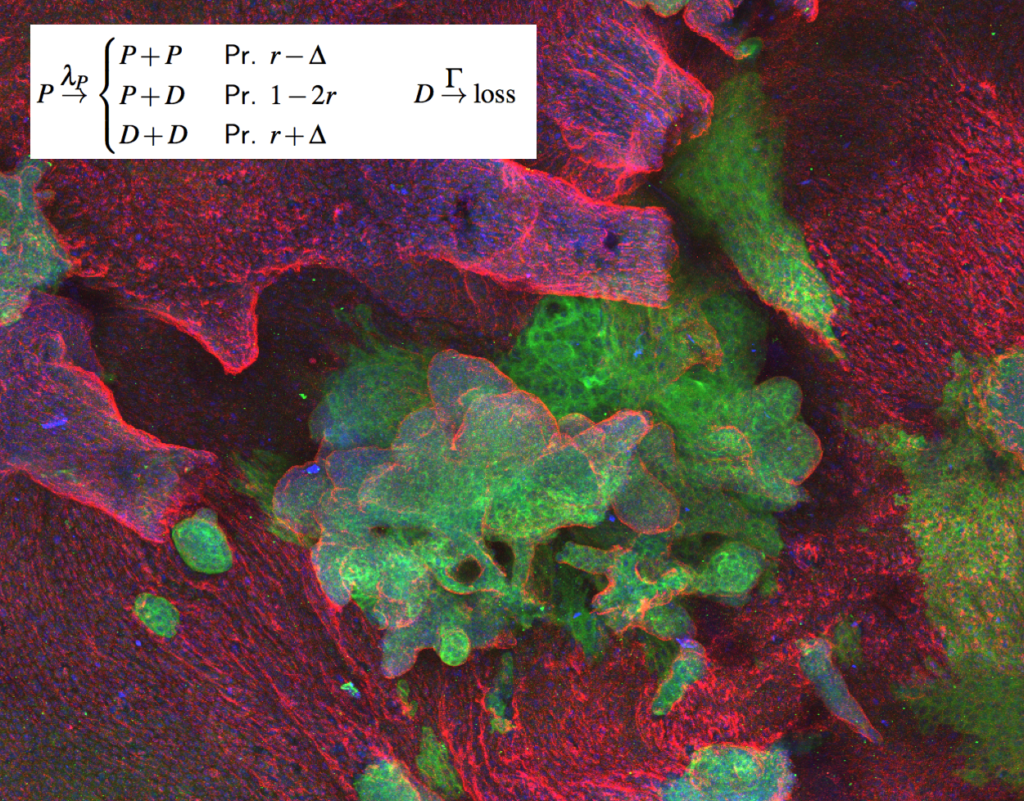
The fate of a single stem cell (during development, homeostasis or cancer initiation) is often profoundly stochastic. Nevertheless, at the population level, cells must “know” how to make the right decisions spatio-temporally. These collective dynamics are still fundamentally ill-understood, and we are approaching it with the tools of statistical physics (at the cell level) and mechanics (at the tissue level). See Sanchez-Danes et al, Nature, 2017, Scheele et al, Nature, 2017; Corominas-Murtra et al, PNAS, 2020 or Azkanaz et al, Nature, 2022)
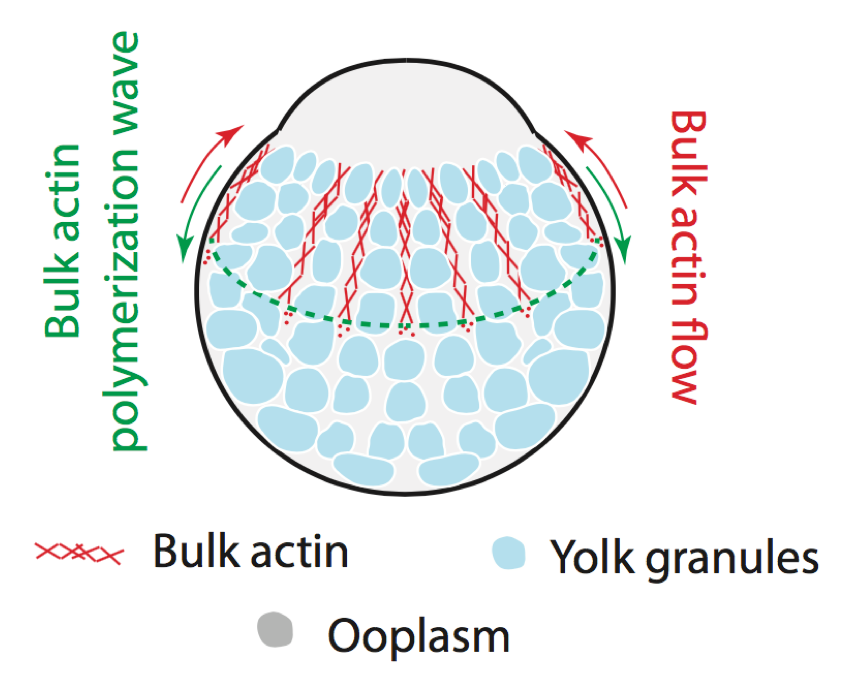
The cell cytoskeleton is a fascinating example of an out-of-equilibrium material. We want to understand the interplay between its mechanical properties and underlying biochemical networks (Hannezo et al, PNAS, 2015 or Qin et al, Nat. Comm. 2018 for instance). We are also interested in how such networks can sense and response to mechanical forces (Pinheiro et al, Nature, 2017), and interact with other cellular components to drive phase seggregation (Shamipour et al, Cell, 2019). Funded by a FWF Standalone Grant.

We are modelling the coupled mechanical and biochemical oscillations that have been observed in multiple in vitro and in vivo epithelial layers (Boocock et al, Nat Phys, 2020 & PRX Life, 2023). We propose that this arises from an instability involving positive feedbacks between ERK/MAPK activity, cellular shape and active tensions. Furthermore, we develop a theory for how cells can use these patterns to break symmetry in the presence of a free edge, and perform wound-healing optimally.
Funding for our group:
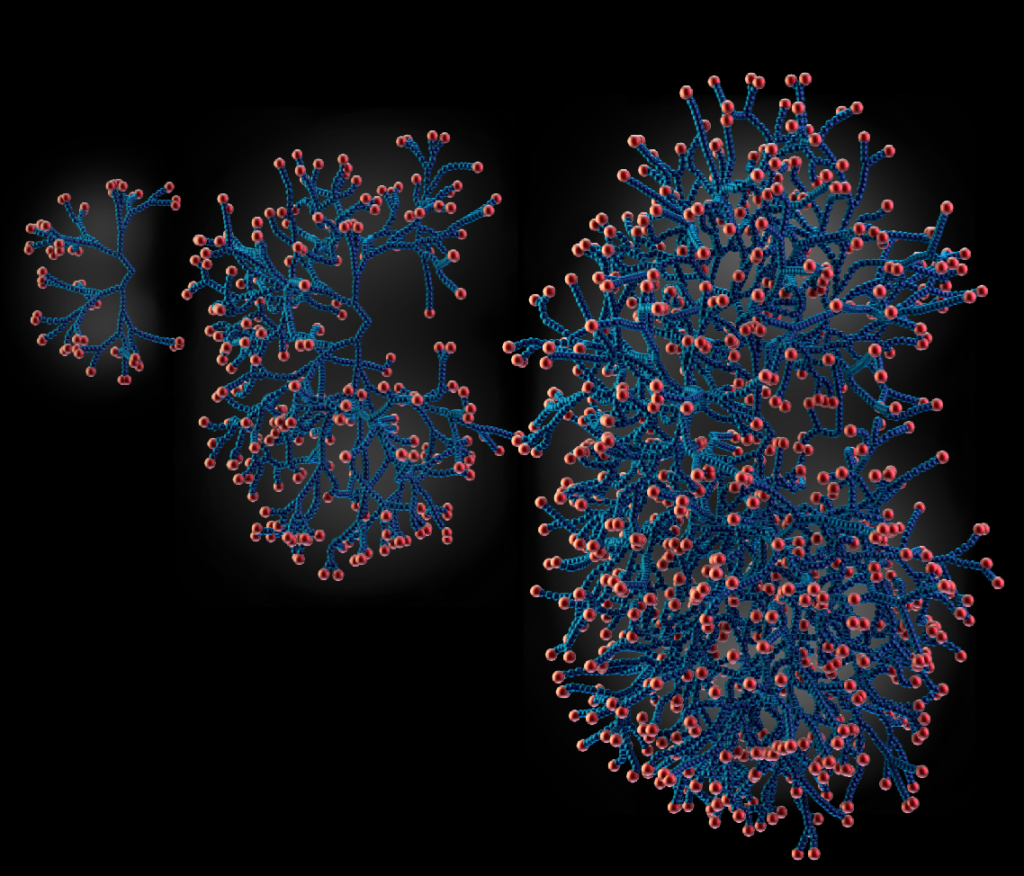
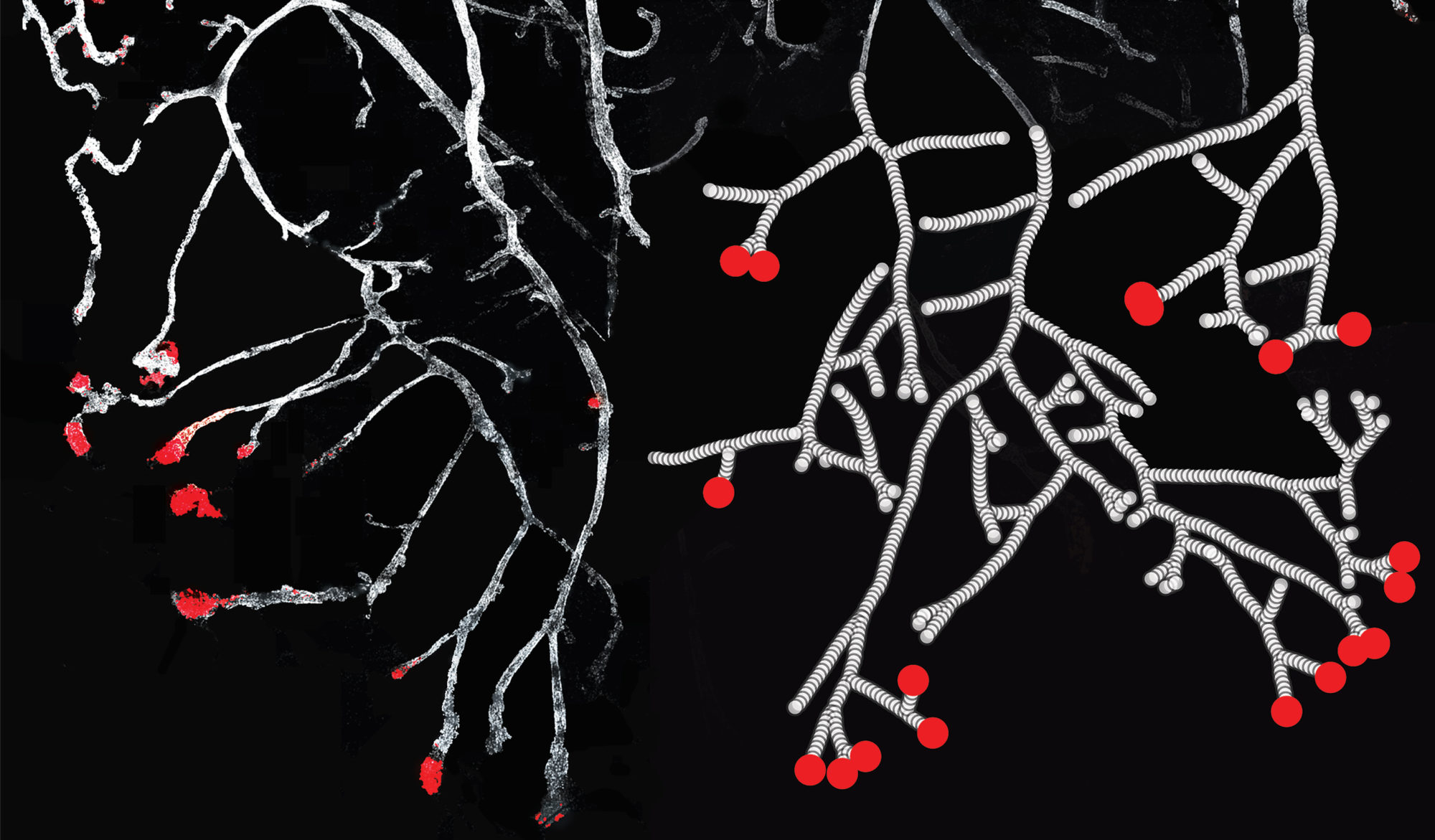
How does complex tissue architecture derive from simple self-organising principles? We use models from out-of-equilibrium statistical physics to derive quantitative principles of branched organ development (see Hannezo et al, Cell, 2017 for instance). This maps in particular to multicomponent branching and annihilating random walks, which allows for self-organization from simple time-invariant and isotropic rules. We are exploring this in multiple multicellular organs, as well as neurons (Ucar et al, Nat Comm, 2021 & Nat Comm, 2023). Funded by an ERC Starting grant.
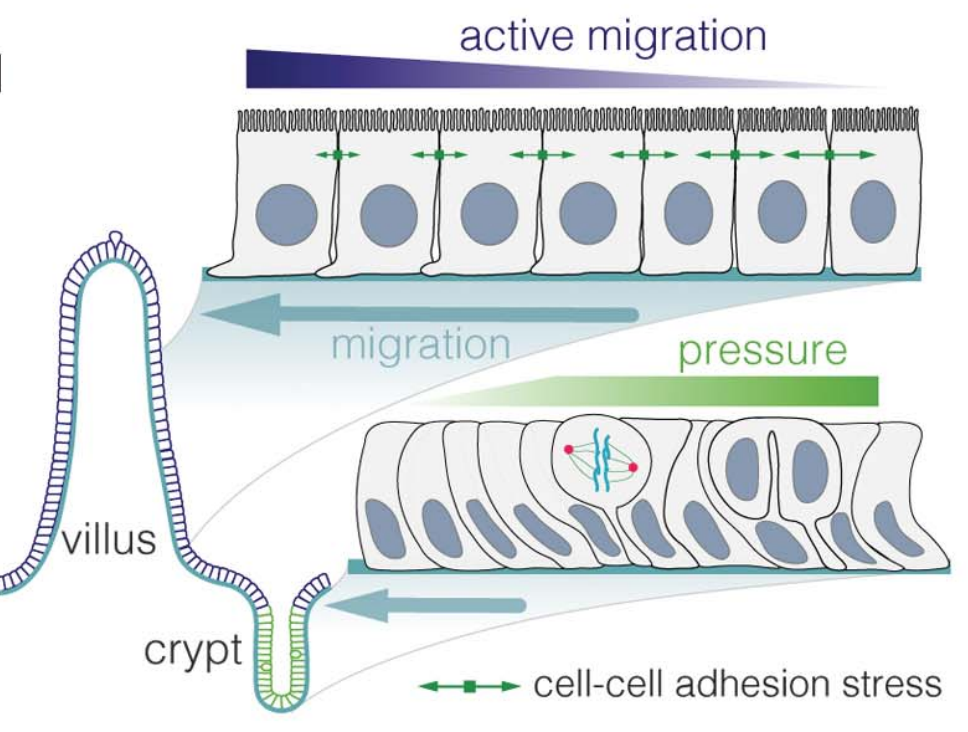
We are interested in understanding how cells migrate collectively, which requires a coordination of both cell-cell and cell-substrate forces. We develop theories to infer migratory forces from in vivo situations, such as intestinal renewal (Krndija et al, Science 2019), but also to understand how cells collectively decide on a directionality, despite intra-cellular noise, cellular variability, and environmental disorder.